bubble_sort خوارزمية الفرز الفقاعي

بسم الله الرحمن الرحيم

ذكرنا في مقالٍ سابقٍ (خوارزمية البحث الثنائي) مثالًا عن أهمية ترتيب العناصر ضمن بنية تخزين المعطيات كالمصفوفة مثلاً، إذًا الغاية من خوارزميات الفرز (الترتيب) هي ترتيب أو فهرسة العناصر تصاعديًا أو تنازليًا. يمكن أن تكون هذه العناصر مجموعات من الأعداد، أو المحارف، أو أي بنيةٍ تحوي أحد هذه الأنماط.

للفرز أنواع عدّة منها: الفرز بالاختيار، والفرز بالإضافة، والفرز بالدمج، والفرز السريع، والفرز الفقاعيّ، وغيرها من الخوارزميات التي سنأتي على ذكرها في المقالات القادمة.

في هذا المقال سنبدأ بخوارزمية الفرز الفقاعي التي سُمّيت كذلك، ببساطة، لأن العناصر في هذه الخوارزمية تستقر في مكانها الصحيح بطريقةٍ تشبه فقاعة الهواء التي تعلو خارج الماء، فلنرَ كيف ذلك!

إقرأ أيضا: خوارزمية البحث الثنائي – Binary Search

ما هي خوارزمية الفرز الفقاعي؟

خوارزمية الترتيب الفقاعي هي خوارزميةٌ مبنيةٌ على فكرة المقارنة المتكررة بين زوجٍ من العناصر المتجاورة، وتبديل مواقعهم إذا كانوا في ترتيبٍ خاطئ.

ما هي آلية عمل الخوارزمية؟

فلنفترض أنّ لدينا مصفوفة A غير مرتبةٍ تحتوي على n عنصر، والمطلوب هو ترتيب العناصر تصاعديًا، فلنفرض أنّ المصفوفة تحتوي على العناصر الآتية: {7, 4, 5, 2}

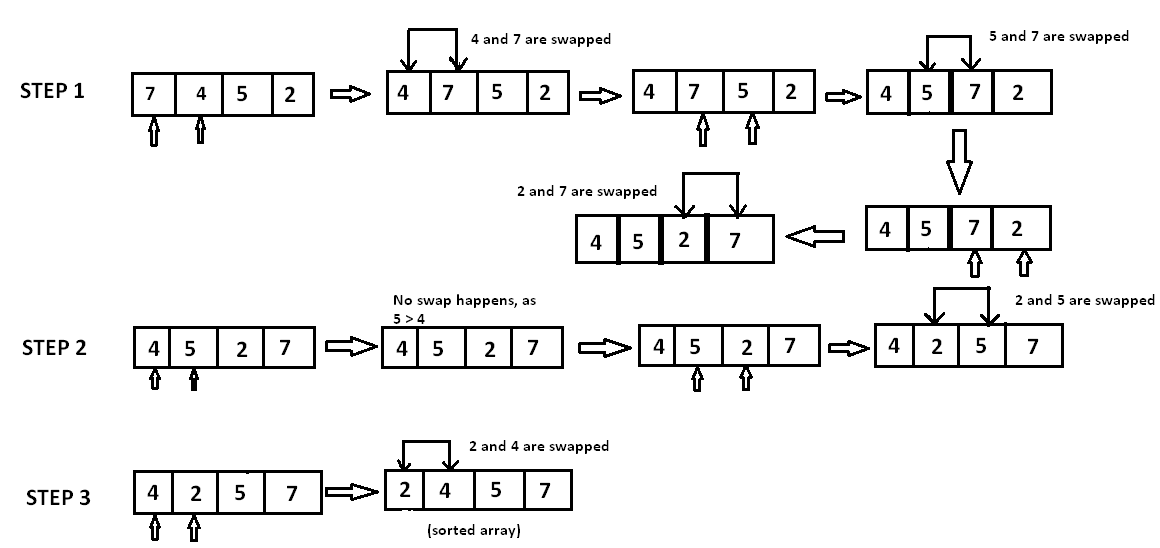
في الخطوة الأولى: مقارنة الرقم 4 مع الرقم 7، وبما أنّ 4 < 7، سيتم تبديل موقعيهما فيما بينهما، ولأن باقي العناصر أصغر من الـ 7، ستكرر العملية حتى يصبح رقم 7 في آخر المصفوفة.

الآن أصبحت المصفوفة بالشكل الآتي : {4, 5, 2, 7}

في الخطوة الثانية: مقارنة الرقم 5 مع الرقم 4 ، وبما أنّ 4 < 5، ومرتبين ترتيبًا تصاعديًا لن يتم تبديل موقعيهما. ثم مقارنة الرقم 5 مع الرقم 2، طبعًا بما أنّ 2 < 5، سيتمّ تبديل موقعيهما فيما بينهما.

الآن أصبحت المصفوفة بالشكل الآتي: {4, 2, 5, 7}

في الخطوة الثالثة: مقارنة الرقم 4 مع الرقم 2، بما أنّ 2 < 4، سيتمّ تبديل موقعيهما فيما بينهما. لتصبح المصفوفة مرتبةً تصاعديًا بالشكل التالي: {2,4,5,7}.

مثالٌ برمجيٌّ لتوضيح آلية العمل:

void bubble_sort( int A[ ], int n ) {
    int temp;
    for(int k = 0; k< n-1; k++) {
        // (n-k-1) is for ignoring comparisons of elements which have already been compared in earlier iterations

        for(int i = 0; i < n-k-1; i++) {
            if(A[ i ] > A[ i+1] ) {
                // here swapping of positions is being done.
                temp = A[ i ];
                A[ i ] = A[ i+1 ];
                A[ i + 1] = temp;
            }
        }
    }
}

view raw bubble_sort.cpp ❤ by Excellent Programmer

درجة تعقيد الخوارزمية (Time Complexity):

تعقيد تربيعيO(n2) من رتبة n2: لأنه يتمّ المرور على كامل المصفوفة من أجل كل عنصر (أي: قراءة n عنصر n مرة).

Excellent programmer

nmbjhmbv n

bubble_sort خوارزمية الفرز الفقاعي

ما هي خوارزمية الفرز الفقاعي؟

ما هي آلية عمل الخوارزمية؟

مثالٌ برمجيٌّ لتوضيح آلية العمل:

درجة تعقيد الخوارزمية (Time Complexity):

	void bubble_sort( int A[ ], int n ) {
	int temp;
	for(int k = 0; k< n-1; k++) {
	// (n-k-1) is for ignoring comparisons of elements which have already been compared in earlier iterations

	for(int i = 0; i < n-k-1; i++) {
	if(A[ i ] > A[ i+1] ) {
	// here swapping of positions is being done.
	temp = A[ i ];
	A[ i ] = A[ i+1 ];
	A[ i + 1] = temp;
	}
	}
	}
	}