خورزمية الفرز بالاختيار selection

بسم الله الرحمن الرحيم 

إنّ الغاية من خوارزميات الفرز (الترتيب) هي ترتيب أو فهرسة العناصر تصاعدياً أو تنازلياً، يمكن أن تكون هذه العناصر مجموعات من الأعداد، أو المحارف، أو أي بنية تحوي أحد هذه الأنماط.

تحدّثنا في مقال سابق عن خوارزمية الفرز الفقاعي (Bubble Sort)، الآن سنكمل في سلسلتنا ونبدأ بالحديث عن خوارزمية الفرز بالاختيار (Selection Sort).

ماهي خوارزمية الفرز بالاختيار؟

خوارزمية الفرز بالاختيار هي خوارزمية مبنية على فكرة إيجاد العنصر الأصغر أو الأكبر من بين مجموعة العناصر غير المرتبة الموجودة في المصفوفة، ومن ثمّ وضعه في الموقع المناسب ضمن المصفوفة.

ماهي آلية عمل الخوارزمية؟

فلنفترض أنّ لدينا مصفوفة A غير مرتبة تحتوي على n عنصر، والمطلوب هو ترتيب العناصر تصاعدياً، فلنفرض أن المصفوفة تحتوي على العناصر الآتية : {7 , 5 , 4 , 2}

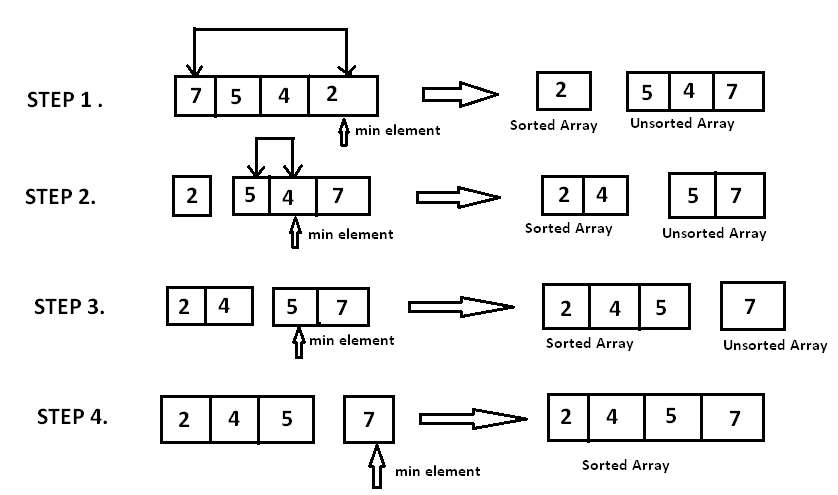
أولاً؛ نبحث عن العنصر الأصغر في المصفوفة (في مثالنا هو الرقم 2). ثانيًا؛ نقوم بالتبديل بينه وبين العنصر الذي يقع في الخانة الأولى من المصفوفة (في مثالنا هو الرقم 7). الآن، نبحث عن العنصر الأصغر من بين العناصر المتبقية من المصفوفة ونضعه في الخانة الثانية، وهكذا دواليك حتى يتم ترتيب جميع العناصر تصاعديًا.

مثال برمجي لتوضيح آلية العمل:

	void selection_sort (int A[ ], int n) {
	// temporary variable to store the position of minimum element
	int minimum;
	// reduces the effective size of the array by one in each iteration.
	for(int i = 0; i < n-1 ; i++) {
	// assuming the first element to be the minimum of the unsorted array .
	minimum = i ;
	// gives the effective size of the unsorted array .
	for(int j = i+1; j < n ; j++ ) {
	if(A[ j ] < A[ minimum ]) { //finds the minimum element
	minimum = j ;
	}
	}
	// putting minimum element on its proper position.
	swap ( A[ minimum ], A[ i ]) ;
	}
	}

view raw

SelectionSort.cpp  ❤ by Excellent  Programmer

درجة تعقيد الخوارزمية (Time Complexity)

تعقيد تربيعيO(n2).

السبب: لإيجاد العنصر الأصغر من بين N عنصر تحتاج إلى N-1 عملية مُقارنة، وبعد وضعه في المكان المناسب (عملية تبديل واحدة) يتبقى N-1 عنصر بحاجة إلى ترتيب. ولإيجاد العنصر الأصغر من بينها تحتاج إلى N-2 مُقارنة، وهكذا. وبالتالي، النتيجة هي:

(N-1) + (N-2) + … +1 = (N . (N-1)) / 2 (عدد عمليات المقارنة)

N  (عدد عمليات التبديل)

لتكون النتيجة النهائية من رتبة O(n2)